I have been pondering a post on heteroskedasticity in this series for a good long while, but I just wasn’t convinced I had much to add. But reading the Wiki entry for heteroskedasticity this past weekend, I realized I might have something to tell those people who have more book knowledge of econometrics than they have practical knowledge of econometrics–a situation which probably describes most graduate students.
First off, what is heteroskedasticity? It is an issue that arises when the variance of the error term e in
Y = a + bX + e
is nonspherical. Seeing as to how this isn’t exactly helpful, a more intuitive explanation is the following:
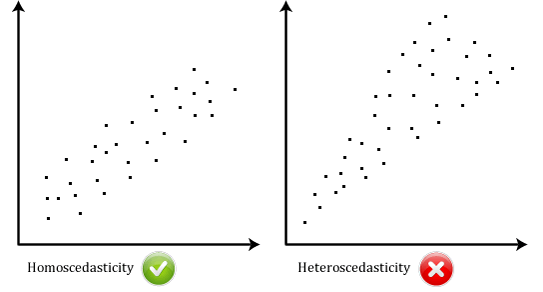
Technically speaking, you have a heteroskedasticity problem when the variance of your error term is nonconstant between observations.
An example I like to use to talk of heteroskedasticity is the following: If you were to regress the demand for sushi on income on, you’d likely see some heteroskedasticity. People with low income tend to have a fairly low consumption of sushi, and there are relatively few departures from the average. People with high income tend to have a higher consumption of sushi, but there are many departures from the average because even among high-income people, some people might dislike sushi, and some people might really like it, which would make a regression of the demand for sushi on income look like the graph on the right-hand side above.
One of the issues with heteroskedasticity lies in how it is often taught as an econometric problem among many. That is, it is not uncommon for grad students to think of heteroskedasticity as no less of a problem than endogeneity, since both problems with lead to the OLS estimator no longer being BLUE.
In practice, however, heteroskedasticity is much less of a problem, for two reasons. First, it is easier to deal with heteroskedasticity than it is to deal with endogeneity. In the context of a linear regression, it is very easy to estimate using a technique that will make your standard errors robust to heteroskedasticity of an unknown form. Dealing with endogeneity is much more difficult: It requires an instrumental variable, a research design with a clearly exogenous source of variation, etc.
Second, heteroskedasticity does not bias your estimate of b above–it merely makes the OLS estimator not be the best (i.e., minimum variance) among linear unbiased estimators. Though one might not be wrong in arguing that this is no less of a problem than dealing with a biased estimator, it turns out that what we care about these days is the identification of causal relationships, which is related to getting an unbiased estimator (or, if one’s estimator is biased, it should be biased in a direction which strengthens the case for there being a causal relationship).
So all this amounts to heteroskedasticity being less severe of a problem than what one might prima facie believe when sitting in econometrics classes.
So when is heteroskedasticity a bit more of a problem? From the Wiki entry on heteroskedasticity:
For any nonlinear model (for instance logit and probit models), however, heteroskedasticity has more severe consequences: the maximum likelihood estimates of the parameters will be biased (in an unknown direction), as well as inconsistent (unless the likelihood function is modified to correctly take into account the precise form of heteroskedasticity). As pointed out by Greene, “simply computing a robust covariance matrix for an otherwise inconsistent estimator does not give it redemption. Consequently, the virtue of a robust covariance matrix in this setting is unclear.”
Or, as Dave Giles has pointed out a long time ago: You can’t just add “, robust” at the end of your “logit” and “probit” commands in Stata and call it a day, because as the excerpt above indicates, in such contexts, you have to correctly specify the form of the heteroskedasticity you’re dealing with. Given the popularity of nonlinear estimators among graduate students (who often seem to prefer using “fancier” MLE-based estimators, because fancier simply appears to translate into “better”), this needs to be emphasized and, for me, it militates in favor of estimating linear probability models (which can accommodate standard errors robust to general forms of heteroskedasticity) over probits and logits.