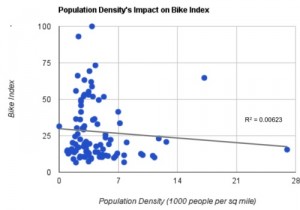
At first we were convinced that 100 percent of the variance in bike market size could be explained by the population density of a city. If you live an a densely populated area like San Francisco, bicycling is an efficient way to get around the city. If you live in Los Angeles, getting on a bicycle can’t really get you anywhere. To our surprise, population density has a nearly zero correlation with our bicycle index. If anything, it very weakly suggests the more densely populated the city, the less prevalence of biking.
That’s from a post titled “The Fixie Bike Index,” on the Priceonomics Blog.
If, like me, you are nowhere near hip enough to know what a fixie is, let me spare you a Google search: a fixie is a fixed-gear bicycle, which is apparently a much-coveted item among hipsters. That’s right: grown men and women enjoy riding around town on a bike like the one you and I used to ride when we were 8 years old.
That being said, let’s go back to the image above. Note how the above-referenced post explains how “population density has a nearly zero correlation with our bicycle index,” which, “[i]f anything, (…) very weakly suggests the more densely populated the city, the less prevalence of biking.”
I guess someone missed the lecture on how sensitive the mean is to outliers back in college. A quick look at the scatter plot and regression line above indicate that the latter is driven by the point on the far right.
Remove that point, and it looks like there might be a positive relationship between a city’s bike index and the density of its population. Trim all four outliers, and it’s really not obvious what is going on.
Surely there’s a bookshop in Williamsburg that has a used copy of Kennedy’s Guide to Econometrics for sale?
(HT: @mungowitz‘s snark, which is not to be confused with Echidna’s Arf.)
On the (Mis)Use of Regression Analysis: Country Music and Suicide
This article assesses the link between country music and metropolitan suicide rates. Country music is hypothesized to nurture a suicidal mood through its concerns with problems common in the suicidal population, such as marital discord, alcohol abuse, and alienation from work. The results of a multiple regression analysis of 49 metropolitan areas show that the greater the airtime devoted to country music, the greater the white suicide rate. The effect is independent of divorce, southernness, poverty, and gun availability. The existence of a country music subculture is thought to reinforce the link between country music and suicide. Our model explains 51 percent of the variance in urban white suicide rates.
That’s the abstract of an article published in Social Forces — a top-10 journal in sociology — in 1992.
Before my snark gets me into trouble: Yes, I do realize that the article was published in 1992, back when most social science researchers only had a flimsy grasp of identification and causality. I also realize it would be foolish to impose on the authors of the above-referenced article the same standards of identification we impose upon ourselves today.
Yet, I cannot help but think that someone with a lesser of understanding of causality than the average reader of this blog is bound to eventually stumble upon the abstract, think “Hey, that totally makes sense!,” and run with it.
I’m sure there are also examples of such findings in other disciplines. If you know of any, please share.
(HT: Friend and former student Norma Padron, who is doing her PhD at Yale and has just launched a nice health economics blog.)