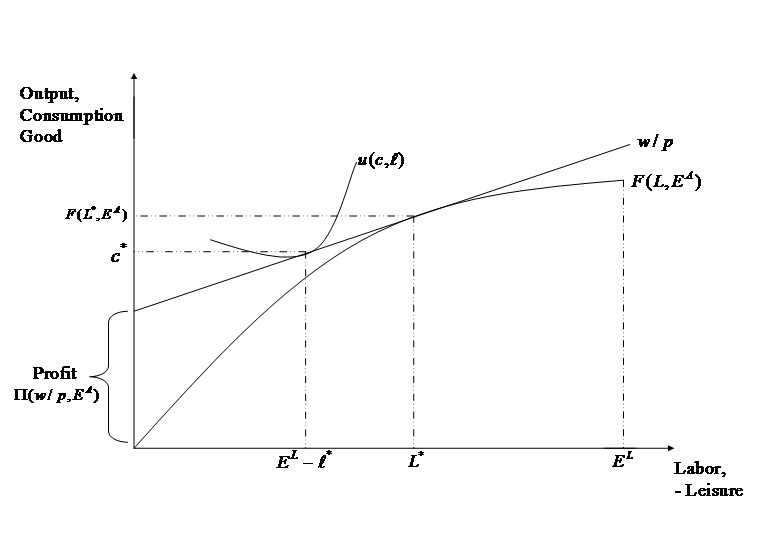
Refer to the figure above, and consider the unitary agricultural model and the case where the Separation Property (Singh et al., 1986) holds, which we discussed in lecture.
The household produces a quantity [math]q=F(L,E^A)[/math] of a staple crop, where [math]L[/math] denotes a household’s labor allocation and [math]E^A[/math] denotes its endowment of land, which we assume fixed in this case. The household consumes a quantity [math]c[/math] of the staple crop. The household also has an endowment of labor time [math]E^L[/math], which it allocates among on-farm labor [math]L[/math], leisure [math]\ell[/math], and market labor [math]L^m[/math], though do note that the household can also hire in labor if it needs to, and that hired labor is denoted [math]L^h[/math]. The household faces wage [math]w[/math] and staple price [math]p[/math].
Pick one of the following three changes in the household’s economic circumstances:
- An increase in the household’s labor endowment, possibly as a result of one of the household’s children attaining adulthood. In other words, the household’s preference structure for consumption and labor remains the same, but the household simply has more labor time,
- An increase in the price of the staple paired with a decrease in the prevailing wage, or
- The adoption of better soil fertility management practices.
Illustrate the change you choose in a graph, and discuss its consequences for the household. Make sure your answer completely describes what happens to the economic circumstances of the household and provides some intuition (or brief explanations) as to why variables change the way they do as a consequence of the change you pick.

The Inverse Farm Size–Productivity Relationship: “Proof” that Smallholders Can Feed the World?
I spent the last week in Montreal for the McGill Global Food Security Conference, where I had been asked to present some of the work I have been doing on food prices.
The conference was very interesting, and it allowed me to finally meet colleagues whom I only knew through their work, meet new colleagues, and interact with a number of students interested in food policy.
At some point, however, one of the presenters mentioned the inverse relationship between farm size (i.e., the amount of land a farmer cultivates) and productivity (i.e., the amount of output per unit of land a farmer can get, or that farmer’s yield), an empirical regularity in the developing world which constitutes an old puzzle in development economics and on which I have done some work a few years ago. The following figure is an example of such a relationship for rice farms in Madagascar — the y-axis measures the logarithm of a plot’s yield in kilograms of rice for one hundredth of a hectare, and the x-axis measures a plot’s size in hundredths of a hectare.
What that presenter said was that the existence of an inverse relationship between farm size and productivity is proof that smallholders can feed the world. Nothing, however, could be further from the truth.